想法、创意与实践

0%

R语言|逻辑回归模型建模案例（交通事故预测）

发表于 更新于 分类于 ， ，
本文字数： 8.3k 阅读时长 ≈ 8 分钟

所有的模型都是错的，但是有用 🌟

本文介绍如何建立逻辑回归模型进行交通事故预测，并验证了模型的准确度。

一、问题描述与数据准备

1.1 问题描述

  基于交通事故相关数据，建立逻辑回归模型，并尽可能使模型的预测准确度达到最高。

  使用交通事故发生前的车辆速度变化值、道路流量的变化值和天气的类型（下雨/晴天），建立回归模型对是否发生交通事故（事故/非事故）进行预测。

1.2 数据导入与类型转换

1.2.1 数据读取

原始数据可通过百度网盘下载：数据下载

使用read.csv（）函数读取CSV格式数据

1
2
# 读取数据
SourceData <- read.csv("C:/Users/Fred/R_project/GLM_dataModel/data 1.csv")

1.2.2 数据类型转化

原始数据类型如下表所示，需要将case和weather均转换为无序因子型的数据。

表1-1 原始数据分析
变量名
数据类型
变量描述
case
int
是否发生事故，1：事故，0：非事故
spd_dif_1min
Num
事故发生前0-1分钟内的速度变化值
spd_dif_2min
Num
事故发生前1-2分钟内的速度变化值
spd_dif_3min
Num
事故发生前2-3分钟内的速度变化值
spd_dif_4min
Num
事故发生前3-4分钟内的速度变化值
vol_dif_1min
Num
事故发生前0-1分钟内的流量变化值
vol_dif_2min
Num
事故发生前1-2分钟内的流量变化值
vol_dif_3min
Num
事故发生前2-3分钟内的流量变化值
vol_dif_4min
Num
事故发生前3-4分钟内的流量变化值
Weather
int
1（下雨），0（晴天）

使用factor（）函数实现类型转换，代码实现如下。

1
2
3
  ## 将case、weather转换为因子型变量，表示类型
nonNA_Data$case <- factor(nonNA_Data$case,levels = c(0,1),labels = c("非事故","事故"))
nonNA_Data$Weather <- factor(nonNA_Data$Weather,levels = c(0,1),labels = c("晴天","下雨"))

二、数据预处理

2.1 统计冗余数据

首先检查是否含有冗余数据，使用duplicated（）函数对原始数据进行判断，检查发现无重复数据。

1
2
  ##冗余数据处理
duplicated_count <- sum(duplicated(SourceData))# 结果无重复数据

2.2 缺失值分析及处理

2.2.1 缺失值分析

在得到数据集后，我们需要观察数据的分布情况，因为很多的模型对缺失值敏感，因此观察是否有缺失值是其中很重要的一个步骤。在正式分析前，我们先通过图形进行对观测字段的缺失情况有一个直观的感受。

  使用VIM包中的aggr（）函数对缺失值进行图形探究。

1
2
library("VIM")
aggr(SourceData,prop=FALSE,numbers = TRUE)
图2-1 aggr()生成的原始数据集的缺失值模式图形

aggr()函数不仅绘制每个变量的缺失值数，还绘制每个变量组合的缺失值数。红色表示缺失，不含缺失值的实例有759个，有缺失值的实例36个；可以看出前4分钟的速度变化值缺失值最多有11个。

使用matrixplot()函数可以生成每个实例数据的图形。

1
matrixplot(SourceData)
图2-2 原始数据集按实例（行）展示真实值和缺失值的矩阵图

此处，数值型数据被重新转换到[0, 1]区间，并用灰度来表示大小：浅色表示值小，深色表示值大。默认缺失值为红色

2.2.2 缺失值插补

对于缺失值的处理方法非常多，例如基于聚类的方法，基于回归的方法，基于均值的方法，其中最简单的方法是直接移除，但是在本文中因为缺失值所占比例较高，直接移除会损失大量观测，因此并不是最合适的方法。在这里，我们使用KNN方法对缺失值进行填补。

1
2
3
4
    ### 删除（异常值）case为空的记录
nonNA_Data <- SourceData[-which(is.na(SourceData$case)),]
    ### 使用kNN方法对缺失值填补
nonNA_Data <- knnImputation(nonNA_Data,k=10,meth = "weighAvg")

2.3 异常值分析及处理

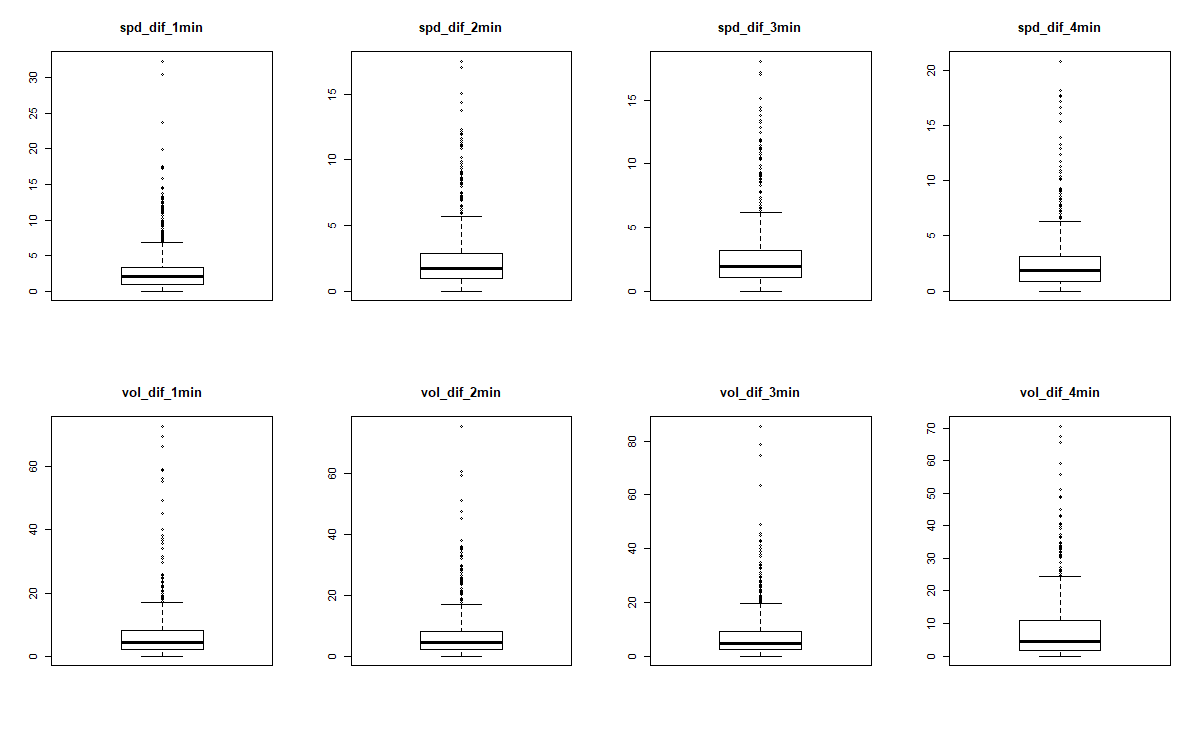
使用箱型图对各个单因素变量进行异常值的分析，结果如下，发现并无明显的异常值。

图2-3 异常值分析

三、变量分析

3.1 单变量分析

主要分析各个变量的分布，使用ggplot2包中的ggplot（）函数绘制各变量的分布统计图如下图。为了简洁，只展示两个变量。

1
2
3
4
5
library(ggplot2)
opar <- par(no.readonly = TRUE)
par(mfrow = c(2,4))
ggplot(df.train, aes(x = spd_dif_1min, y = ..density..)) + geom_histogram(fill = "blue", colour = "grey60", size = 0.2, alpha = 0.2) + geom_density()
ggplot(df.train, aes(x = spd_dif_2min, y = ..density..)) + geom_histogram(fill = "blue", colour = "grey60", size = 0.2, alpha = 0.2) + geom_density()
图3-1 变量分布统计图

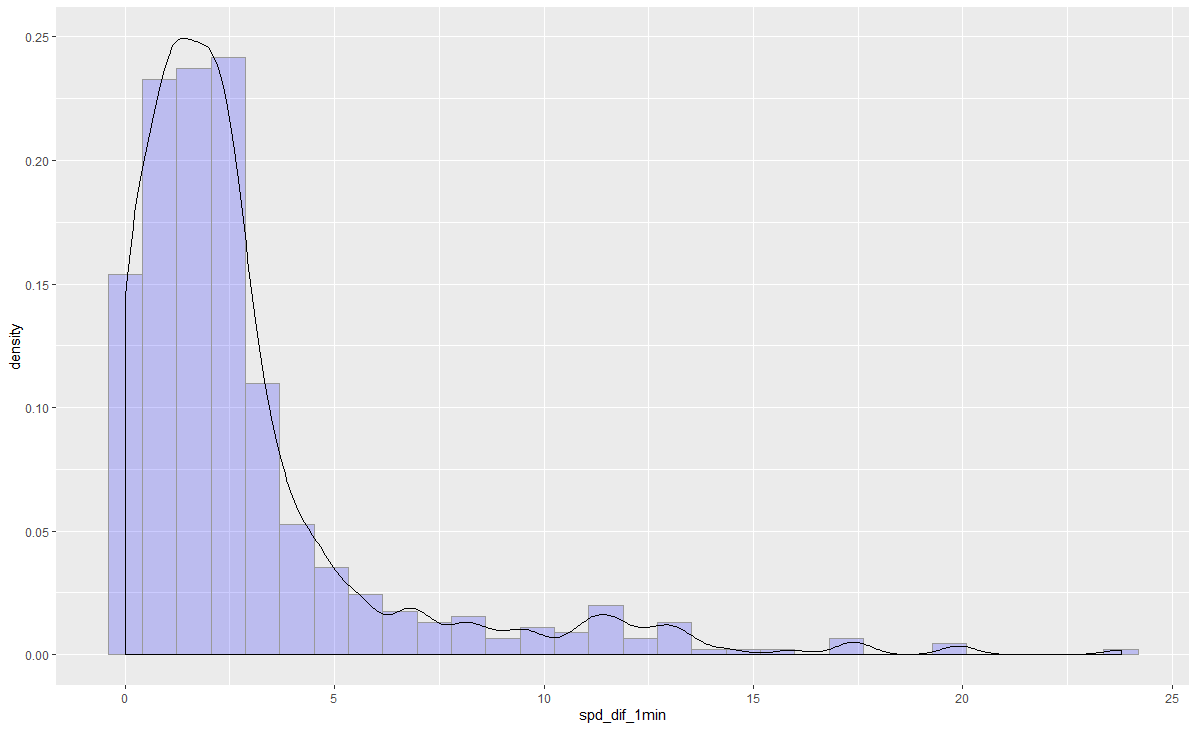
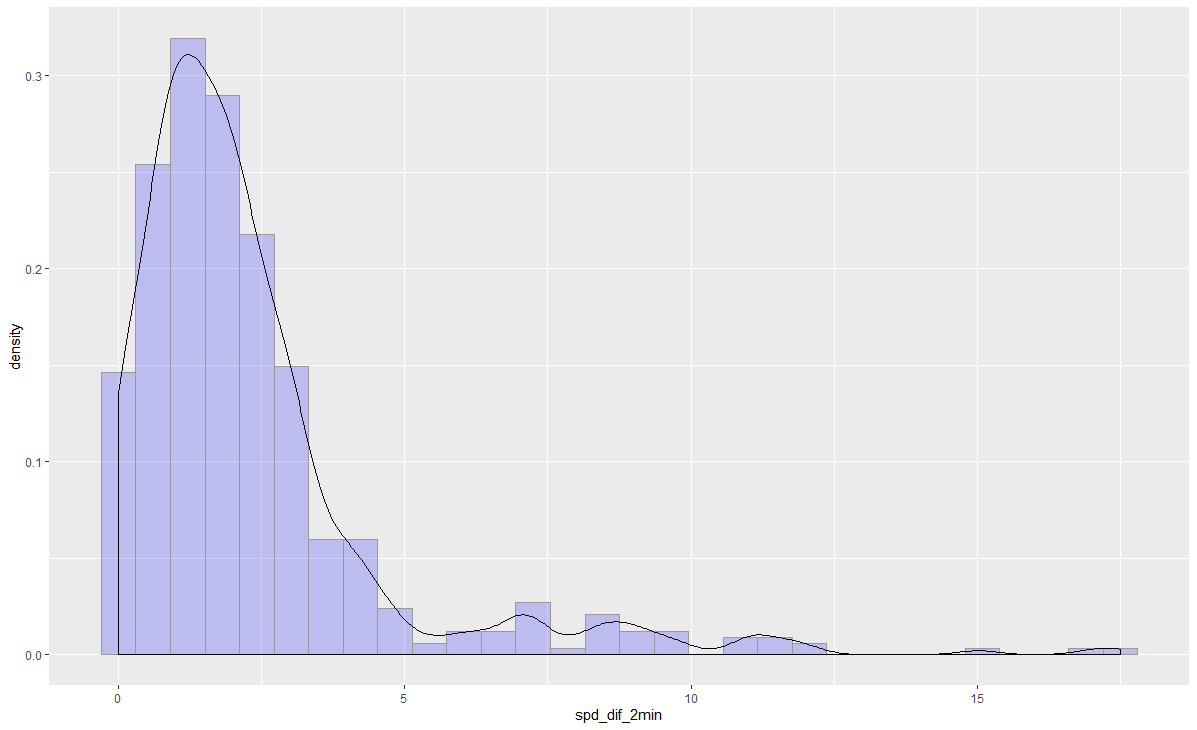
可以看出，各个变量的分布大致呈负指数分布。

3.2 多变量之间的相关性分析

建模之前首先得检验变量之间的相关性，如果变量之间相关性显著，会影响模型的预测效果。下面通过corrplot函数，画出各变量之间，包括响应变量与自变量的相关性。由下图可以看出，各变量之间的相关性是非常小的。

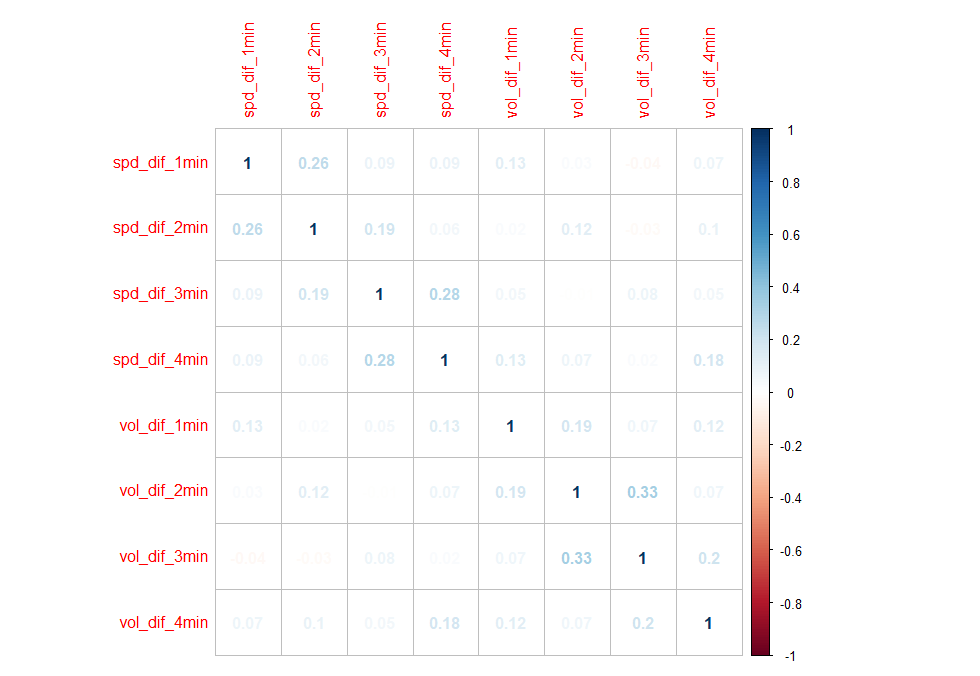
图3-2 变量之间的相关性分析
1
2
3
library(corrplot)
cor1<-cor(nonNA_Data[,2:9])
corrplot(cor1,method = "number")

四、Logistic回归建模

4.1 数据集分割

将样本分为按照模型标定：模型校验=7:3的比例划分。nrow（x）返回x对象的序号，Sample（）函数随机抽取70%的序号，由此完成数据分割。

1
2
3
4
train <- sample(nrow(nonNA_Data), 0.7*nrow(nonNA_Data))
  ## 表示从数据集中随机抽取70%的数据的序号
df.train <- nonNA_Data[train,]
df.validate <- nonNA_Data[-train,]

4.2 建立模型

首先将所有自变量都考虑放入模型中，进行Logistic回归建模，模型如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
fit.full <- glm(case~spd_dif_1min + spd_dif_2min + spd_dif_3min + spd_dif_4m
in + vol_dif_1min + vol_dif_2min + vol_dif_3min + vol_dif_4min + Weather, da
ta = df.train, family = binomial(link = 'logit'))
 summary(fit.full)
 ## Call:
 ## glm(formula = case ~ spd_dif_1min + spd_dif_2min + spd_dif_3min +
 ## spd_dif_4min + vol_dif_1min + vol_dif_2min + vol_dif_3min +
 ## vol_dif_4min + Weather, family = binomial(link = "logit"),
 ## data = df.train)

 ## Deviance Residuals:
 ## Min 1Q Median 3Q Max
 ## -1.6603 -0.6247 -0.4932 -0.4031 2.2398

 ## Coefficients:
 ## Estimate Std. Error z value Pr(>|z|)
 ## (Intercept) -2.93342 0.27208 -10.781 < 2e-16 ***
 ## spd_dif_1min 0.13201 0.03045 4.335 1.46e-05 ***
 ## spd_dif_2min 0.02350 0.04661 0.504 0.6141
 ## spd_dif_3min 0.06076 0.04150 1.464 0.1431
 ## spd_dif_4min 0.09812 0.04155 2.361 0.0182 *
 ## vol_dif_1min 0.02697 0.01127 2.394 0.0167 *
 ## vol_dif_2min 0.02265 0.01301 1.742 0.0815 .
 ## vol_dif_3min 0.01161 0.01170 0.993 0.3209
 ## vol_dif_4min 0.01010 0.01142 0.884 0.3767
 ## Weather 下雨 0.15360 0.37075 0.414 0.6787
 ## ---
 ## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

 ## (Dispersion parameter for binomial family taken to be 1)

 ## Null deviance: 544.17 on 554 degrees of freedom
 ## Residual deviance: 487.01 on 545 degrees of freedom
 ## AIC: 507.01

 ## Number of Fisher Scoring iterations: 4

从summary（）返回的结果看出，自变量spd_dif_1min、spd_dif_4min和vol_dif_1min对方程的贡献度较为显著，而其他变量对方程的贡献度不显著，去除这些变量，检验新模型是否拟合得好：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
fit.reduced <- glm(case ~ spd_dif_1min + spd_dif_4min + vol_dif_1min, data =
df.train, family = binomial(link = 'logit'))
 summary(fit.reduced)

 ## Call:
 ## glm(formula = case ~ spd_dif_1min + spd_dif_4min + vol_dif_1min,
 ## family = binomial(link = "logit"), data = df.train)

 ## Deviance Residuals:
 ## Min 1Q Median 3Q Max
 ## -1.8244 -0.6018 -0.5241 -0.4484 2.1127

 ## Coefficients:
 ## Estimate Std. Error z value Pr(>|z|)
 ## (Intercept) -2.44831 0.20239 -12.097 < 2e-16 ***
 ## spd_dif_1min 0.13722 0.02938 4.670 3.01e-06 ***
 ## spd_dif_4min 0.12250 0.03863 3.171 0.00152 **
 ## vol_dif_1min 0.03197 0.01114 2.871 0.00410 **
 ## ---
 ## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

 ## (Dispersion parameter for binomial family taken to be 1)
 ## Null deviance: 544.17 on 554 degrees of freedom
 ## Residual deviance: 496.79 on 551 degrees of freedom
 ## AIC: 504.79

 ## Number of Fisher Scoring iterations: 4

新模型的每个回归系数都非常显著（p<0.05）。由于两模型嵌套（fit.reduced是fit.full的一个子集），可以使用anova()函数对它们进行比较，对于广义线性回归，可用卡方检验。

1
2
3
4
5
6
7
8
9
10
anova(fit.reduced, fit.full, test = "Chisq")
 ## Analysis of Deviance Table

 ## Model 1: case ~ spd_dif_1min + spd_dif_4min + vol_dif_1min
 ## Model 2: case ~ spd_dif_1min + spd_dif_2min + spd_dif_3min + spd_dif_4min+
 ## vol_dif_1min + vol_dif_2min + vol_dif_3min + vol_dif_4min +
 ## Weather
 ## Resid. Df Resid. Dev Df Deviance Pr(>Chi)
 ## 1 551 496.79
 ## 2 545 487.01 6 9.7794 0.1343

结果的卡方值不显著（p=0.1343），表明三个预测变量的新模型与九个完整预测变量的模型拟合程度一样好。添加其他6个变量不会显著提高方程的预测精度，因此可以依据更简单的模型进行解释。

解释模型参数：

1
2
3
exp(coef(fit.reduced))
## (Intercept) spd_dif_1min spd_dif_4min vol_dif_1min
## 0.08643927 1.14708542 1.13031911 1.03248943

可以看到，1min内速度的变化量增加1个单位，事故发生的优势将乘以1.14708542，同理1min速度、2min流量的变化量增加一个单位，事故发生的优势将乘以1.13031911、1.03248943。

4.3 判定标定模型的拟合优度

  通常一个二值分类器可以通过ROC（Receiver Operating Characteristic）曲线和AUC值来评价优劣。

  很多二元分类器会产生一个概率预测值，而非仅仅是0-1预测值。我们可以使用某个阈值（例如0.5），以划分哪些预测为1，哪些预测为0。得到二元预测值后，可以构建一个混淆矩阵来评价二元分类器的预测效果。所有的训练数据都会落入这个矩阵中，而对角线上的数字代表了预测正确的数目，即true positive + true negative。同时可以相应算出TPR（真正率或称为敏感度）和TNR（真负率或称为特异度）。我们主观上希望这两个指标越大越好，但可惜二者是一个此消彼涨的关系。除了分类器的训练参数，阈值的选择，也会大大的影响TPR和TNR。有时可以根据具体问题和需要，来选择具体的阈值。

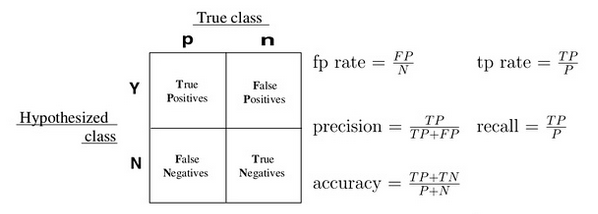
首先使用训练数据集生成概率预测值：

1
2
library(pROC)
 pre <- predict(fit.reduced,type='response',df.train)

需要特别注意的是：type一定要加，否则计算的最优阈值为负数

下面使用pROC包计算fit.reduced模型的拟合优度：

1
2
3
4
5
modelroc <- roc(df.train$case,pre)
plot(modelroc, print.auc=TRUE, auc.polygon=TRUE, 
     grid=c(0.1, 0.2), grid.col=c("green", "red"),
     max.auc.polygon=TRUE,
     auc.polygon.col="skyblue", print.thres=TRUE)
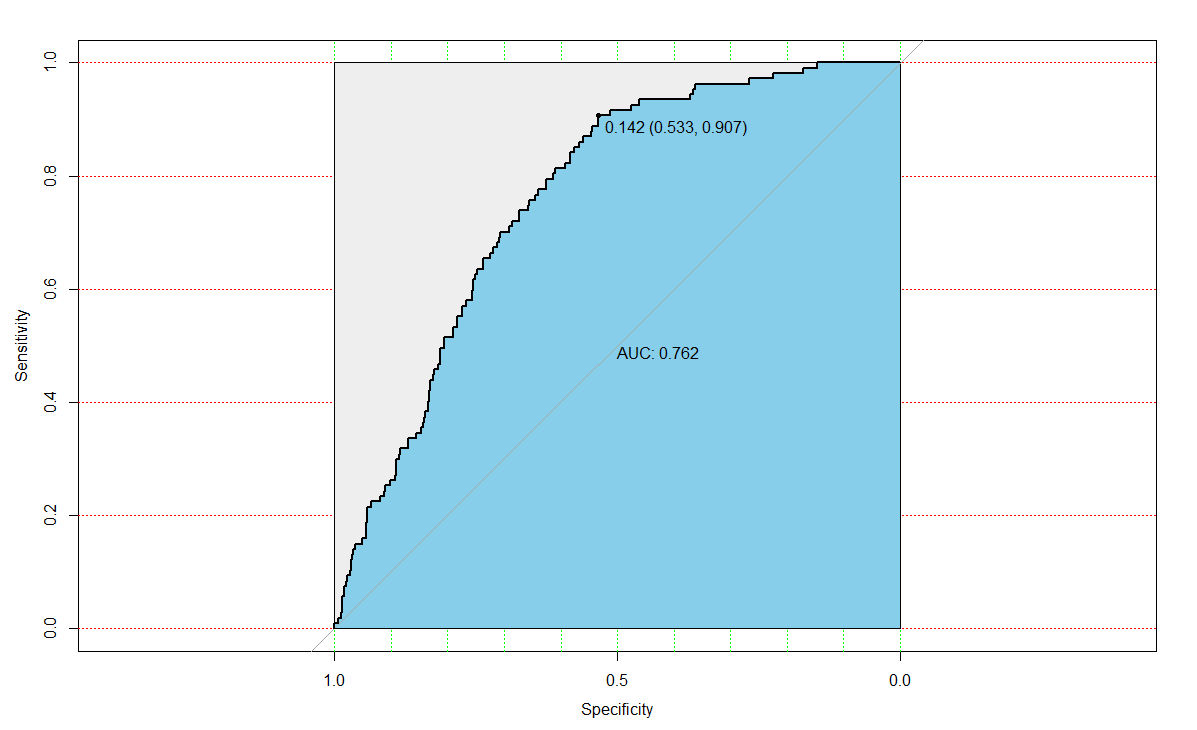
图4-1 拟合优度ROC

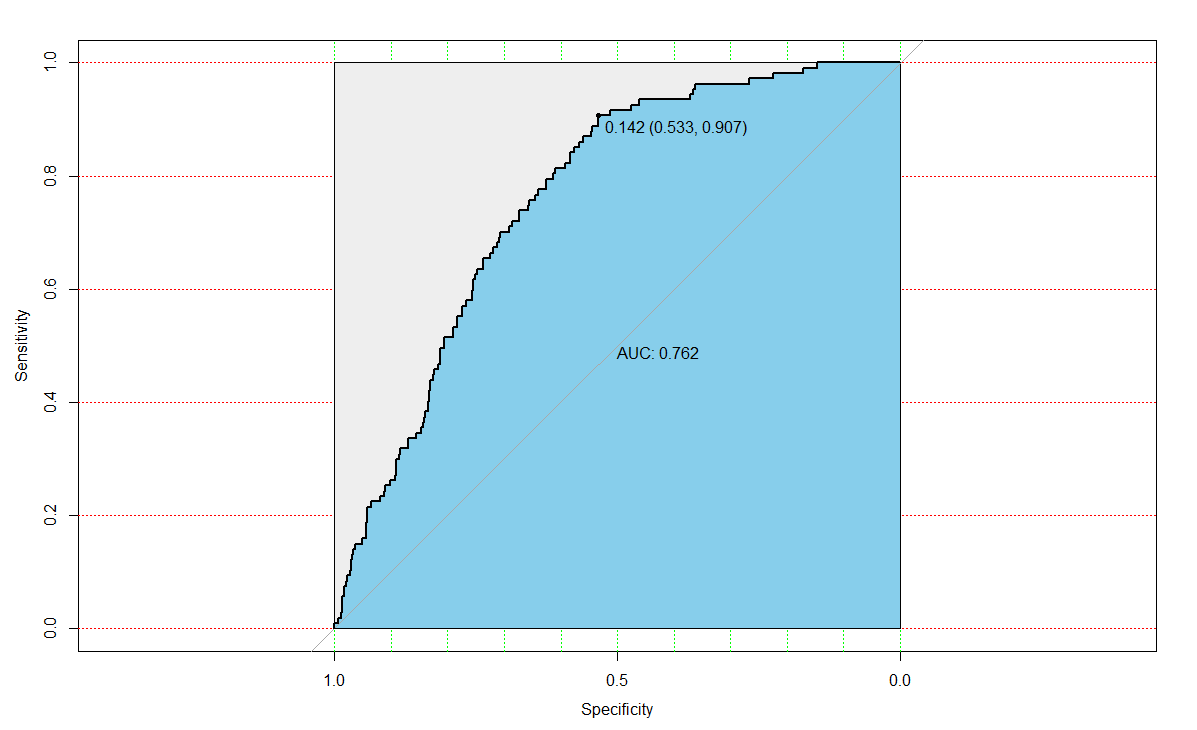
从图中可以看出阈值为0.142时，对应的AUC（Area Under Curve）值为0.762大于0.7，区分能力可以接受，还有提高的空间。阈值为0.142，对应的敏感度和特异度分别为：0.907、0.533。

五、评估模型的预测效果

基于测试集使用建立的模型计算预测值，与真值比较计算出预测的准确率：

1
2
3
4
5
6
# 评估模型的预测效果
 predict <- predict(fit.reduced,type='response',newdata=df.validate)
 predict.results <- ifelse( predict> 0.142,"事故","非事故")
 ## 错误率
 misClasificError <- mean(predict.results != df.validate$case)
 print(paste('准确率',1-misClasificError))

计算的准确率为 0.62343，准确率不是很高🙈，可以考虑重新设计模型的结构提高准确率。

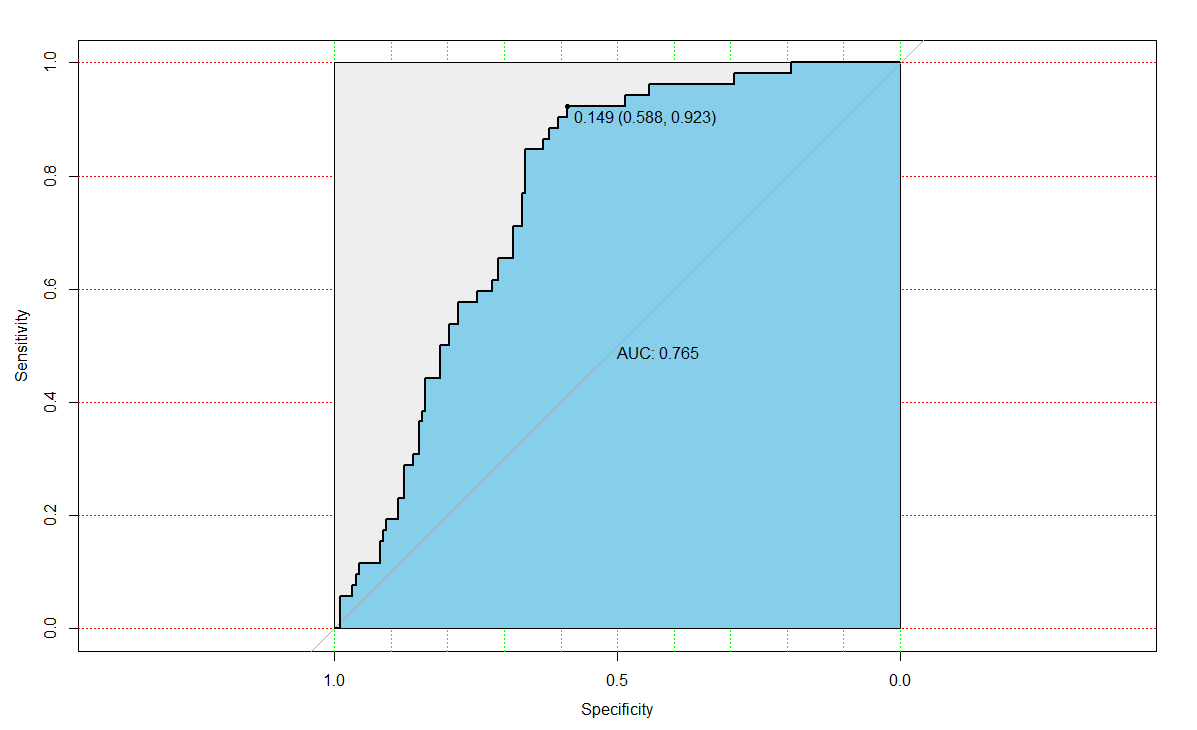
使用测试数据集计算ROC拟合优度，对于测试数据集AUC为0.765，TPR为0.923，TNR为0.588。

1
2
3
4
5
6
7
# 测试集的ROC拟合优度
validate_pre <- predict(fit.reduced,type='response',df.validate)
validate_roc <- roc(df.validate$case,validate_pre)
plot(validate_roc, print.auc=TRUE, auc.polygon=TRUE, grid=c(0.1, 0.2),
     grid.col=c("green", "red"), max.auc.polygon=TRUE,
     auc.polygon.col="skyblue", print.thres=TRUE)
  ## AUC = 0.765, TPR = 0.923, TNR = 0.588,阈值 = 0.149
图5-1 测试数据集拟合优度

总结

  通过这个案例对广义线性模型中的logistics回归模型有了初步的了解,练习了数据预处理（建模准备）、建立模型、评价模型的完整过程😎。

参考文献

[1] Kabacoff R , 卡巴科弗, Kabacoff, et al. R 语言实战[M]. 人民邮电出版社, 2013.

[2] 如何在R语言中使用Logistic回归模型

[3] 信用卡评分

[4] logistic回归预测婚姻出轨|R语言

留言区欢迎任何的建议与批评💡~
如果你觉得这篇文章对你有用，欢迎分享、打赏哦☕~